2019年，全国工业用水量为1 217.6 亿m³，占到全国用水总量的20.2%，万元工业增加值用水量为38.4 m³，超过了发达国家的2倍，与当前国际先进工业用水水平仍有较大的差距。工业节水是通过工业水的循环使用、串级使用、处理再用，来提高工业用水的效率，进一步降低工业用水量。

目前常规的用水网络的研究，主要集中在新鲜水用量优化方法上，包括水夹点法和数学规划法。

在1980年国外学者就首次将数学规划方法用于工业用水系统的用水优化配置，以实现工业水的串级使用。之后有研究者对传质型用水网络提出了一种利用杂质负荷曲线和供水负荷曲线的夹点来确定最小新鲜水用量的办法——水夹点法（water pinch）。

2002年，冯霄等将水夹点技术用于国内工业用水系统的分析中。针对水夹点方法在处理超结构水网络以及多杂质水系统优化问题中的不足，国内学者开展了多角度多层次的研究，不断地对水系统集成理论及方法进行完善。

刘永健等针对单组分杂质用水和废水处理网络同步集成优化问题，以最小总操作费用为目标，建立了非线性规划模型进行求解。

刘永忠等针对水系统集成优化中的新鲜水用量、用水系统的柔性和用水网络结构复杂程度三方面的目标，提出利用博弈理论对水网络优化方案分析的方法。

丁力等为了解决优化后的水网结构复杂的问题，建立了冷却塔循环水量最小、流股数最少的多目标水系统优化模型，能够得到结构相对简单的用水网络。

韩政针对循环冷却系统中回水重用问题，构建了最大回用冷却水为目标的水网优化模型。李爱红针对水网络中的多杂质问题，提出了具有再生单元的多杂质间歇过程用水水网络集成方法。

工业用水系统优化研究方面，前人主要围绕水质指标进行节水优化研究，弱化了各个用水单元的需水量以及排水量因素，得到的复杂水网络模型难于指导实践。

笔者针对前人研究中出现的不足，以整个工业水系统为研究对象，根据不同的用水功能将工业用水系统划分为若干个特定的子系统，通过构建基于各用水子系统的供需水关系的水系统优化模型，以用水成本最小为目标进行优化配置，运用沃格尔（Vogel）最佳路径分析方法求解最优水量分配方案，最后对节水优化带来的综合效益进行了分析。

1 模型构建

1.1 问题描述

若供工业用水系统中有m个独立水源分别为Ai（i=1，2，…，m），包括一次水源、二次水源和补充水源，各个水源的可供水量为ai；根据不同的用水功能将工业用水系统划分为图片n个用水子系统Bj（j=1，2，…，n），各个用水子系统的需水量为图片bj；水源图片Ai将可供水量ai分配给各用水子系统Bj，各用水子系统得到的水量为图片xij，分配水量的单位成本为图片图片Cij。

基于梯级用水的工业水系统优化问题是一个关于图片m个水源、n个用水部门的水量优化分配问题。该模型的目标是合理确定水源图片Ai分配到用水子系统Bj图片的水量xij图片，使得整个工业水系统的用水总成本最低。

1.2 数学建模

基于梯级用水理念的工业水系统优化模型目标函数一般形式如下：

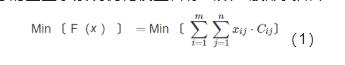
式中：图片xij图片为第i个水源图片图片Ai分配到第j个用水子系统图片Bj图片的水量，m³/h；Cij图片为水源图片Ai给用水户Bj图片单方水的配水成本单价，元/m³；i=1，2，…，m；j=1，2，…，n。

配水成本单价Cij图片图片是优化模型中非常重要的参数，数值直接影响到配水量xij图片图片的数值，从水源图片Ai把单位水量分配到用水子系统Bj图片所需的费用图片Cij图片图片由水处理费用和输送费用两部分组成。

水处理费用的确定由水源和用水子系统的水质差距决定，差距越大，水处理费用越高，其包括水资源税费、药剂费、工人工资、设备折旧费和维护检修费等。在此研究中，厂区内的输送费用不计，补给水源考虑输水费用。

1.3 约束条件

式中：图片图片xij为水源图片Ai图片给用水户图片Bj分配的水量；ai为第i图片个水源图片Ai图片的可供水量；图片bj为第j图片个用水子系统Bj图片的需水量；i=1，2，…，m；j=1，2，…，n。

用水单元数据见表1。

1.4 求解方案

基于梯级用水的工业水系统优化模型当各水源的排水总量与各用水单元的需水总量相等时，可以视为供需平衡的运输问题，若供需不平衡则需要通过特定的处理将问题转换为供需平衡问题，可以使用Vogel法对模型进行优化求解；求解可按过程分为，模型实例化、利用Vogel法进行求解、结果的分析与验证。

模型实例化需要结合企业梯级用水方案进行具体分析，确定需要优化的单元，也可针对用水子系统进行两层优化。

如果优化问题为供需不平衡的问题可以通过模型层面添加假想的用水单元（外排水），或通过机理层面优化单元排水将问题转换为供需平衡问题，本研究案例使用转换措施为后者。

待优化单元的需水量以及排水量需要根据梯级用水方案以及稳定状态下的单元运行数据进行确定，用水单元间的配水成本需要对企业历史运行数据进行分析，将各方面的成本进行累加得到总的单位配水成本，构建模型所需的数据与表1所需数据一致。

Vogel法求解工业水系统优化问题计算步骤为：

（1）计算用水单元数据表中各行各列最小以及次小配水成本（图片Cij图片图片）的差额。

（2）在所有行差额、列差额中找出最大的差额，按差额最大者进行最小配水成本优先分配水量（如果遇到最大差额有多个，任选1个）。即选择最大差额所在行或列的最小配水成本Ci,j图片图片图片，令对应位置的决策变量图片xi,j图片图片图片取最大值。

（3）调整剩余供应量或需求量缺口，图片ai,2图片图片=图片ai,1-xi,j, bj,2图片图片=图片bj,1-xi,j。

（4）重复（1）、（2）、（3），直至{ai,n图片图片=图片0图片｝，{bj,n图片图片=图片0图片｝，所有的需求量缺口均被满足，对应用水数据表中供需水量均为0。最后将未调整的图片xi,j均赋为0。

（5）对优化结果进行验证，查看是否存在奇异值。

基于优化的结果，与生产实际进行对应，调整不合理的用水路径，并得到最终的用水网络，即为当前梯级用水情景下的最佳水网流通路径。

2 案例分析

选取山西省某火力发电厂作为典型工业水系统进行优化，电厂总装机容量为3 300 MW，机组日取地下水水量约70 000 m³，一期建成机组采用逆流式自然通风冷却塔冷却，二期建成机组采用间接空冷冷却，脱硫系统采用的是“石灰石-石膏”湿法烟气脱硫技术，电厂各用水系统存在一定的节水空间。

电厂存在364 m³/h的直接外排水量，为供需不平衡问题，现通过节水设计和运行优化将该水系统处理为供需平衡水系统。

2.1 用水现状分析

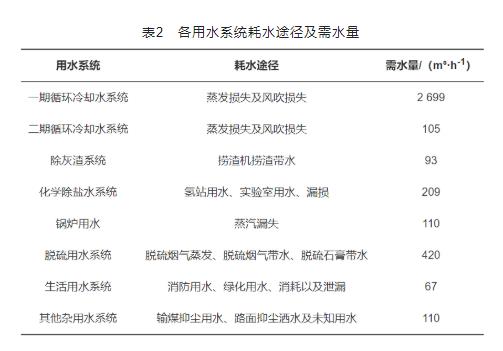
通过水平衡测试可知，全厂新鲜水取用量为3 255 m³/h，总用水量为230 235 m³/h，其中循环水量为226 362 m³/h，回用水量为618 m³/h，重复用水量226 980 m³/h；循环水率为98.32%，重复利用率为98.59%；总耗水量为2 891 m³/h，总排水量为364 m³/h，排水率为11.18%。各用水系统水消耗途经及需水量见表2。