摘 要:输气管道气相泄漏速率计算是泄漏风险评估的前提和基础。为此,通过搭建气相管道小孔泄漏实验系统,开展圆孔、周向矩形方孔、轴向矩形方孔的泄漏速率实验,获取了不同裂口几何形态的气相泄漏速率。在此基础上,建立了基于FLUENT的管道孔口泄漏CFD仿真模型,并用其研究了裂口几何形态对中低压管道小孔泄漏速率的影响机理、泄漏孔口附近的气体动力学特征量,包括速度分布、马赫数分布等。仿真结果表明:最大速度发生在泄漏孔口截面中心处,矩形方孔的最大速度明显高于圆孔,而裂口方向对其影响不显著;从临界压力比来看,孔口面积一定,矩形方孔更容易在孔口处达到临界流,圆孔、周向矩形方孔、轴向矩形方孔的临界压力比模拟值均低于理论计算值。该实验结果有助于气相管道小孔泄漏研究的深化,也为气相管道泄漏事故的应急处置提供了参考依据。
关键词:输气管道 小孔泄漏 实验 数值模拟 几何形态 泄漏速率 速度分布 马赫数分布
Impact of a hole¢s geometrical characteristics Oil the aperture leakage of natural gas pipelines
Abstract:Gas leakage rate calculation is the premise of and foundation for leakage risk assessment in natural gas pipelines.An experimental system was established for the small leakage of natural gas pipelines to evaluate the respective leakage rates respectively of round holes,circumferential rectangular square holes and axial rectangular square holes,and to obtain the gas leaking rate of holes with different geometrical characteristics.On this basis,FLUENT-based pipe hole leak CFD simulation was performed to investigate the influence mechanism of hole geometrical characteristics on medium-and low-pressure pipe hole-leaking rate and gas dynamic characteristic quantities,including speed distribution and Mach number distribution.Simulation results showed that the maximum rate was at the cross-section center of a leaking hole,and that the maximum speed of a rectangular hole was significantly higher thanthat of a square hole,but the influence of hole direction was insignificant;and in terms of critical pressure ratio,if the hole area was determined.it is easier for a rectangular square hole to achieve the critical flow;but as for the critical pressure of a round hole,a circumferential rectangular square hole,and an axial rectangular square hole,their analogous values were all lower than theoretical values.The experimental results are of great help to the deepening of gas pipe hole leaking research and provide scientific guidance for the emergency response to gas pipe leakage.
Keywords:gas pipeline,hole-leaking,experiment,numerical simulation,geometrical characteristics,leaking rate,speed distribution,Mach number distribution
随着天然气管网规模的不断扩大,由于各种原因导致的泄漏事故时有发生。泄漏速率计算是天然气管网安全领域的重要问题,也是泄漏后扩散、风险评估的前提和基础。
较早的泄漏速率模型研究主要基于理论推导和数值计算,假设气体在管内为绝热流动,在泄漏点为等熵流动,遵循理想气体状态方程和泊松方程,根据能量守恒和动量守恒方程定量描述管内气体的流动过程。Montiel[1]提出了适用于不同泄漏孔径的管孔综合模型,讨论了管内为亚临界流、孔口为临界流或亚临界流以及管内和孔口均为临界流的泄漏速率计算方法。国内学者[2-4]。通过对Montiel模型的研究发现,管内和孔口均出现临界流的情形在工程实际中很少见。因此在气体泄漏速率计算过程中仅保留前两种情形。这类模型本身存在一定的缺陷,如没有考虑裂口几何形态对泄漏速率的影响,对于理论推导的泄漏速率缺少相应的验证等。
实验和计算流体力学(CFD)可以更详尽地研究管道泄漏的流场特征。赵金辉等吲提出了大孔亚临界流泄漏速率的计算公式,并搭建气体管道泄漏模拟实验台验证公式的正确性和适用性。Kostowski等[6]利用实验和CFD方法比较绝热模型和等温模型的适用性。目前,基于实验和CFD方法研究输气管道泄漏主要针对圆孔,考虑到不同的泄漏部位和破坏原因可能造成不同的裂口形状和方向[7]。因此无法全面描述裂口几何形态对泄漏速率的影响。
笔者的主要研究对象为中低压输气管道因腐蚀等原因引发的小孔泄漏,这主要是因为相对而言,小孔泄漏在实际情况中更难发现与定位[8]。利用相似原理搭建气相管道小孔泄漏实验系统,设计并加工不同的泄漏模块以模拟不同的泄漏场景;以FLUENT为平台建立仿真模型,并对模型的可行性展开全面的理论分析和实验验证,在此基础上研究裂口几何形态对泄漏速率的影响机理并得到泄漏孔口附近的气体动力学特征量,包括速度分布、马赫数分布等,使研究趋于精细化,为管道泄漏事故的应急救援和事故调查提供理论依据。
1 实验方法
1.1 实验系统
利用相似原理搭建气相管道小孔泄漏实验系统,实验过程中以空气为介质,主要是出于安全和成本方面的考虑,尽管天然气与空气性质不同,但并不会影响研究裂口几何形态对泄漏速率的影响。
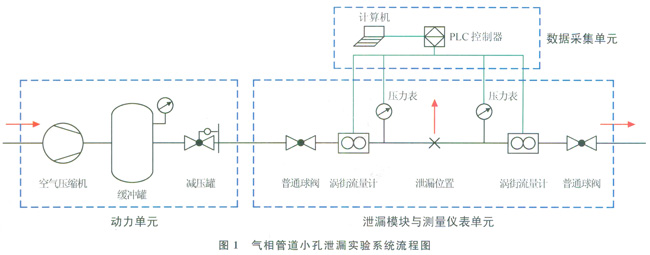
图1为气相管道小孔泄漏实验系统流程图,系统主要由动力单元、泄漏模块与测量仪表单元、数据采集单元组成。其中:
动力单元:包括空气压缩机、缓冲罐、减压阀,为系统提供压力恒定的气源。
泄漏模块与测量仪表单元:包括一套可拆卸更换的泄漏模块以及安装在泄漏模块两端的压力表、涡街流量计,模拟泄漏过程发生及监测过程参数的变化。
数据采集单元:包括PLC控制器、计算机,实现过程参数的实时采集与处理。
实验过程中,空气通过压缩机增压至缓冲罐,经减压阀减压后,在泄漏模块处发生泄漏,未泄漏的空气对大气进行放空;通过安装在泄漏模块两端的压力表和涡街流量计监测压力、流量参数的实时变化;通过泄漏模块两端涡街流量计的差值换算得到泄漏速率[9]。
1.2 技术思路
实验通过调节减压阀、更换泄漏模块等手段构建不同的泄漏场景,研究管内压力、泄漏孔口形状、裂口方向对泄漏速率的影响机理。综合考虑实验的可操作性及相关标准规范,确定具有代表性的孔口尺度与管道压力范围。为尽可能降低读数的观测误差及舍入误差,采用多次实验取平均值的方法。
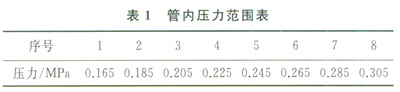
1.3 管内压力
实验所用管道为不锈钢材质,内径50mm,壁厚3.5mm,压力的选取主要依据《城镇燃气设计规范》(GB 50028—2006),结合减压阀的工作特性,确定本实验的管道压力范围,如表1所示。
1.4 泄漏模块
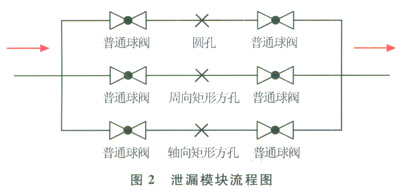
设计并加工一套可拆卸更换的泄漏模块,即3根并联连接的管道,每根管道长1.2m,在管道顶部开圆孔和矩形方孔,圆孔和矩形方孔具有等水力半径的几何特征,矩形方孔的长边沿周向或轴向分布,通过阀门切换管道模拟不同裂口形状及方向的泄漏过程。圆孔孔径为5mm,主要参照《基于风险的检验》(API 581—2008)关于小孔泄漏孔径的推荐范围。图2为泄漏模块流程图。
1.5 实验结果
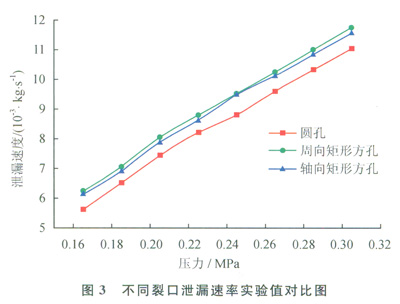
图3为圆孔、周向矩形方孔、轴向矩形方孔的泄漏速率实验值对比。由图3可以看出,对于圆孔、周向矩形方孔、轴向矩形方孔,管内压力增大时泄漏速率随之增加,呈近似线性关系,因为气体通过孔流出的过程可假定为等熵膨胀,孔口面积一定,随着管内压力增大,更多的压力能转化为气体的动能,泄漏速率随之增加。相同的管内压力下,矩形方孔的泄漏速率显著高于圆孔,从实验数据来看,裂口方向对泄漏速率的影响不显著,压力为0.245MPa时,周向矩形方孔与轴向矩形方孔泄漏速率的差值仅为0.0323×10-3kg/s,但总体上,相同的管内压力下,周向矩形方孔泄漏速率略高于轴向矩形方孔。
2 数值仿真
2.1 控制方程及计算方法
流体的流动应遵循质量守恒定律、动量守恒定律和能量守恒定律,而控制方程是上述守恒定律的数学描述。建立气体管道泄漏数值模拟的控制方程组,包括可压缩理想流体的质量守恒方程、动量守恒方程和能量守恒方程,其通用形式是[10]:
从左至右,方程中各项依次为瞬态项、对流项、扩散项、源项。j是通用变量;G是广义扩散系数;S是广义源项。对于特定的方程,j、G、S具有特定的形式。此外,控制方程组还应包括附加的湍流输运方程。u是速度失量。
湍流模型采用标准k-e双方程模型,具有较高的适用性和精度。标准k-e双方程模型假定湍动黏度是各向同性的,基本输运方程为:
式中Gk是由平均速度梯度引起的湍动能k的产生项;Gb是由于浮力引起湍动能k的产生项;YM代表可压湍流中脉动扩张的贡献;C1e、C2e和C3e为经验常数;ak和ae分别为湍动能是和湍流耗散率e对应的Prandtl数;Sk和Se是用户定义的源项。
求解控制方程组采用基于压力的稳态求解器,选择该方法是因为本文主要关心近似稳定状态下的泄漏速率和气体动力学特征量分布,对于中低压输气管道,选择基于压力的求解器可提高计算效率同时可以保证较高的精度。

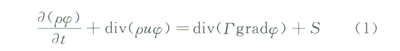
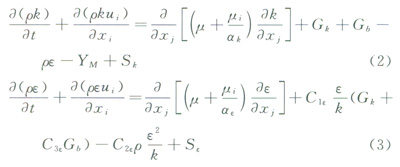
 谈谈化工企业如何做好日常安全管理
谈谈化工企业如何做好日常安全管理 便携式水质分析实验室在纺织行业中的…
便携式水质分析实验室在纺织行业中的… 二次酸洗工艺对垃圾焚烧飞灰重金属脱…
二次酸洗工艺对垃圾焚烧飞灰重金属脱… 功能性固井工作液研究进展
功能性固井工作液研究进展 环氧氯丙烷改性纤维素溶液的流变与减…
环氧氯丙烷改性纤维素溶液的流变与减… 磺基甜菜碱的合成及其在水包油乳化钻…
磺基甜菜碱的合成及其在水包油乳化钻… 精细动态控压固井技术在顺南区块的应用
精细动态控压固井技术在顺南区块的应用 抗高温超分子降滤失剂的合成及性能评价
抗高温超分子降滤失剂的合成及性能评价 长输燃气管道的安全保护距离
长输燃气管道的安全保护距离 危险化学品安全措施和应急处置
危险化学品安全措施和应急处置 加油站重大危险源分级管理与风险控制…
加油站重大危险源分级管理与风险控制… 天然气管道安全置换方法的探讨
天然气管道安全置换方法的探讨 浅谈加油站安全管理
浅谈加油站安全管理 浅议化工企业安全生产管理
浅议化工企业安全生产管理 危化品生产企业安全管理方法
危化品生产企业安全管理方法 化工火灾危险性分析
化工火灾危险性分析